注：此文章同步于wei xin gong zhong hao：“宇你谈市”。

一觉醒来，又多放了一天假，我再不发篇文章，就长草了。今天文章出自我师兄，蚁哥。之前我们在学校，一起绞尽脑汁，“玩命”灌水发Paper的时候，他idea就特别多。先说，此文绝非其他类似的广告宣传，实则友情投文。

下面讲的是关于这次疫情的一次简单的数学建模，我们只是做纯数学的一次未来的推演，当然里面还有很多不确定的因素，不搞科研很久的我，第一次看完之后也是觉得烧脑。你们看呢？

大学算法课和小学奥数中有这样一道经典题：

一上来就很烧脑对不对，我们先来一个月一个月的分析一下：

第1个月：1对兔子；

第2个月：1对兔子；

第3个月：第2个月的1对 + 新生的1对（第1个月的兔子生的） = 2对；

第4个月：第3个月的2对 + 新生的1对（第2个月的兔子生的） = 3对；

第5个月：第4个月的3对 + 新生的2对（第3个月的兔子生的） = 5对；

。

。

。

这道题表现的本质就是斐波那契数列：

这样1到12月小兔子分别有1,1,2,3,5,8,13,21,34,55,89,144。 这跟非典疫情有啥关系，别急，这都是下面数学模型的铺垫。

让我们改造上面这个小学题：

是不是和兔子的问题是一样一样的？那么斐波那契数列就可以变为：

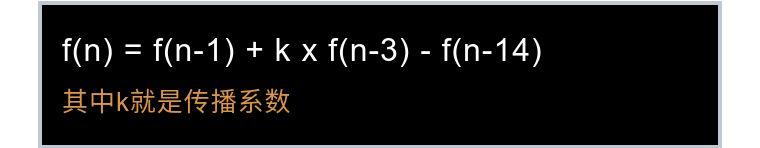
我们命名为14天治愈模型，让我们大致令k=0.33到0.4。0.33这里可以理解为每天每个病人大致传染0.33个人，即每3个现有的病人，就会有一个新的人被感染。算算看，好吓人，如果k=0.36，就能传播17500人。注意k=0.33，大致2600人。

不过，不要担心，我们祖国采取了封城模式，1月24号左右，各地限制了人流。我们可以继续改造这个模型，当n>24，传播系数k=0.7*k，每天衰减为原先的0.7倍。这样有了14天治愈模型（封城）：

看看下面的图，上面的是没有封城的14天治愈模型，下面是使用封城的14天治愈模型。

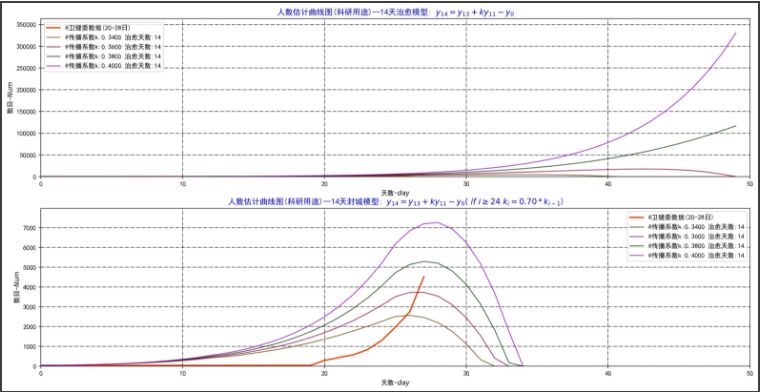
我们对比一下，人数降低了许多不是，所以不要抱怨封城，数据分析告诉我们，此举措能大大降低传播的人数，并缩短疫情的发病时间。

要做一个精确的数学模型，尤其是要和真实数据做到完全拟合非常不容易。后面还有很多工作要做，例如调整治愈天数，传播系数，衰减参数等等。这些暂时超出了我们科普文章的范畴。此文只是作为抛砖引玉，送给对于数学建模感兴趣的投资者，后面的深入工作，就留给大家思考吧。

其实作为量化投资，也一直是我的兴趣和目标。一起努力，用数字完善我们的交易模型吧。

最后还是要感谢在前线一直努力奋斗的医护人员和其他各行各业为了对抗疫情奋战的工作人员，祝愿大家一切安好，平安过年。

注：此文章同步于wei xin gong zhong hao：“宇你谈市”。